Help:Displaying a formula
MediaWiki uses a subset of TeX markup, including some extensions from LaTeX and AMS-Latex, for mathematical formulae. It generates either PNG images or simple HTML markup, depending on user preferences and the complexity of the expression. In the future, as more browsers are smarter, it will be able to generate enhanced HTML or even MathML in many cases.
More precisely, MediaWiki filters the markup through Texvc, which in turn passes the commands to TeX for the actual rendering. Thus, only a limited part of the full TeX language is supported; see below for details.
Technicals
Syntax
Math markup goes inside <math> ... </math>. The edit toolbar has a button for this..
Similar to HTML, in TeX extra spaces and newlines are ignored.
The TeX code has to be put literally: MediaWiki templates, predefined templates, and parameters cannot be used within math tags: pairs of double braces are ignored and "#" gives an error message. However, math tags work in the then and else part of #if, etc.
Rendering
The PNG images are black on white (not transparent). These colors, as well as font sizes and types, are independent of browser settings or CSS. Font sizes and types will often deviate from what HTML renders. Vertical alignment with the surrounding text can also be a problem. The css selector of the images is img.tex.
It should be pointed out that solutions to most of these shortcomings have been proposed but have not been implemented yet.
The alt attribute of the PNG images (the text that is displayed if your browser can't display images; Internet Explorer shows it up in the hover box) is the wikitext that produced them, excluding the <math> and </math>.
Apart from function and operator names, as is customary in mathematics for variables, letters are in italics; digits are not. Other text is not supported.
TeX vs HTML
Before introducing TeX markup for producing special characters, it should be noted that, as this comparison table shows, sometimes similar results can be achieved in HTML (see Help:Special characters).
| TeX Syntax (forcing PNG) | TeX Rendering | HTML Syntax | HTML Rendering |
|---|---|---|---|
<math>\alpha\,\!</math>
|
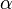
|
{{math|<VAR>α</VAR>}}
|
α |
<math>\sqrt{2}</math>
|
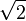
|
{{math|{{radical|2}}}}
|
√2 |
<math>\sqrt{1-e^2}</math>
|
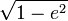
|
{{math|{{radical|1 − ''e''²}}}}
|
√1 − e² |
The codes on the left produce the symbols on the right, but the latter can also be put directly in the wikitext, except for ‘=’.
α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ ς τ υ φ χ ψ ω Γ Δ Θ Λ Ξ Π Σ Φ Ψ Ω | α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ ς τ υ φ χ ψ ω Γ Δ Θ Λ Ξ Π Σ Φ Ψ Ω |
∫ ∑ ∏ √ − ± ∞ | ∫ ∑ ∏ √ − ± ∞ ≈ ∝ = ≡ ≠ ≤ ≥ × · ÷ ∂ ′ ″ ∇ ‰ ° ∴ Ø ø ∈ ∉ ∩ ∪ ⊂ ⊃ ⊆ ⊇ ¬ ∧ ∨ ∃ ∀ ⇒ ⇔ → ↔ ↑ ℵ - – — |
The use of HTML instead of TeX is still under discussion. The arguments either way can be summarised as follows.
Pros of HTML
- In-line HTML formulae always align properly with the rest of the HTML text.
- The formula’s background and font size match the rest of HTML contents and the appearance respects CSS and browser settings while the typeface is conveniently altered to help you identify formulae.
- Pages using HTML code for formulae will load faster and they will create less clutter on your hard disk.
- Formulae typeset with HTML code will be accessible to client-side script links (a.k.a. scriptlets).
- The display of a formula entered using mathematical templates can be conveniently altered by modifying the templates involved; this modification will affect all relevant formulae without any manual intervention.
- The HTML code, if entered diligently, will contain all semantic information to transform the equation back to TeX or any other code as needed. It can even contain differences TeX does not normally catch, e.g.
{{math|''i''}}for the imaginary unit and{{math|<VAR>i</VAR>}}for an arbitrary index variable.
Pros of TeX
- TeX is semantically superior to HTML. In TeX, "
<math>x</math>" means "mathematical variable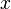 ", whereas in HTML "
", whereas in HTML "x" could mean anything. Information has been irrevocably lost. - On the other hand, if you encode the same formula as "
{{math|<VAR>x</VAR>}}", you get the same visual result x and no information is lost. This requires diligence and more typing that could make the formula harder to understand as you type it. However, since there are far more readers than editors, this effort is worth considering. - TeX has been specifically designed for typesetting formulae, so input is easier and more natural if you are accustomed to it, and output is more aesthetically pleasing if you focus on a single formula rather than on the whole containing page.
- One consequence of point 1 is that TeX code can be transformed into HTML, but not vice-versa.[1] This means that on the server side we can always transform a formula, based on its complexity and location within the text, user preferences, type of browser, etc. Therefore, where possible, all the benefits of HTML can be retained, together with the benefits of TeX. It is true that the current situation is not ideal, but that is not a good reason to drop information/contents. It is more a reason to help improve the situation.
- Another consequence of point 1 is that TeX can be converted to MathML for browsers which support it, thus keeping its semantics and allowing the rendering to be better suited for the reader’s graphic device.
- When writing in TeX, editors need not worry about whether this or that version of this or that browser supports this or that HTML entity. The burden of these decisions is put on the software. This does not hold for HTML formulae, which can easily end up being rendered wrongly or differently from the editor’s intentions on a different browser.[2]
- More importantly, the serif font used for rendering formulae is browser-dependent and it may be missing some important glyphs. While the browser generally capable to substitute a matching glyph from a different font family, it need not be the case for combined glyphs (compare ‘ a̅ ’ and ‘ a̅ ’).
- TeX is the preferred text formatting language of most professional mathematicians, scientists, and engineers. It is easier to persuade them to contribute if they can write in TeX.
 Note:dilHTML unless your wikitext follows the style of point 2
Note:dilHTML unless your wikitext follows the style of point 2
 Note:browsupp The entity support problem is not limited to mathematical formulae though; it can be easily solved by using the corresponding characters instead of entities, as the character repertoire links do, except for cases where the corresponding glyphs are visually indiscernible (e.g. – for ‘–’ and − for ‘−’).
Note:browsupp The entity support problem is not limited to mathematical formulae though; it can be easily solved by using the corresponding characters instead of entities, as the character repertoire links do, except for cases where the corresponding glyphs are visually indiscernible (e.g. – for ‘–’ and − for ‘−’).
Functions, symbols, special characters
Accents/Diacritics | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
\acute{a} \grave{a} \hat{a} \tilde{a} \breve{a}
|
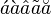
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\check{a} \bar{a} \ddot{a} \dot{a}
|
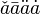
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Standard functions | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\sin a \cos b \tan c
|
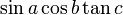
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\sec d \csc e \cot f
|
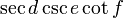
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\arcsin h \arccos i \arctan j
|
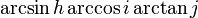
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\sinh k \cosh l \tanh m \coth n\!
|
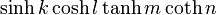
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\operatorname{sh}\,o\,\operatorname{ch}\,p\,\operatorname{th}\,q\!
|
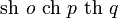
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\operatorname{arsinh}\,r\,\operatorname{arcosh}\,s\,\operatorname{artanh}\,t
|
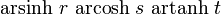
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\lim u \limsup v \liminf w \min x \max y\!
|
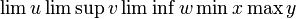
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\inf z \sup a \exp b \ln c \lg d \log e \log_{10} f \ker g\!
|
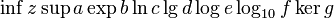
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\deg h \gcd i \Pr j \det k \hom l \arg m \dim n
|
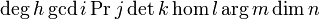
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Modular arithmetic | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
s_k \equiv 0 \pmod{m}
|
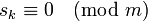
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a\,\bmod\,b
|
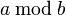
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Derivatives | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\nabla \, \partial x \, dx \, \dot x \, \ddot y\, dy/dx\, \frac{dy}{dx}\, \frac{\partial^2 y}{\partial x_1\,\partial x_2}
|
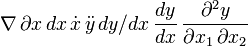
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sets | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\forall \exists \empty \emptyset \varnothing
|
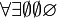
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\in \ni \not \in \notin \subset \subseteq \supset \supseteq
|
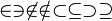
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\cap \bigcap \cup \bigcup \biguplus \setminus \smallsetminus
|
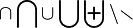
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\sqsubset \sqsubseteq \sqsupset \sqsupseteq \sqcap \sqcup \bigsqcup
|
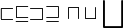
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Operators | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ \oplus \bigoplus \pm \mp -
|
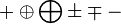
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\times \otimes \bigotimes \cdot \circ \bullet \bigodot
|
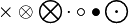
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\star * / \div \frac{1}{2}
|
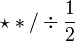
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Logic | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\land (or \and) \wedge \bigwedge \bar{q} \to p
|
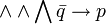
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\lor \vee \bigvee \lnot \neg q \And
|
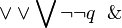
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Root | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\sqrt{2} \sqrt[n]{x}
|
![\sqrt{2} \sqrt[n]{x}\,\!](/wiki/images/math/b/1/c/b1cf10dc44d326999f62708d9999fcc8.png)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Relations | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\approx \simeq \cong \dot= {=}
|
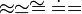
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\le < \ll \gg \ge > \equiv \not\equiv \ne \mbox{or} \neq \propto
|
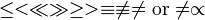
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Geometric | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\Diamond \Box \triangle \angle \perp \mid \nmid \| 45^\circ
|
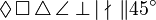
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Arrows | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\leftarrow (or \gets) \rightarrow (or \to) \nleftarrow \nrightarrow \leftrightarrow \longleftarrow \longrightarrow
|
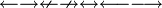
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\Leftarrow \Rightarrow \Leftrightarrow \Longleftarrow \Longrightarrow \Longleftrightarrow (or \iff)
|
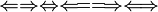
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\uparrow \downarrow \updownarrow \Uparrow \Downarrow \Updownarrow \nearrow \searrow \swarrow \nwarrow
|
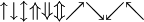
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\rightharpoonup \rightharpoondown \leftharpoonup \leftharpoondown \upharpoonleft \upharpoonright \downharpoonleft \downharpoonright
|
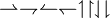
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\mapsto \longmapsto \hookrightarrow \hookleftarrow
|
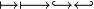
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Special | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\And \eth \S \P \% \dagger \ddagger \ldots \cdots
|
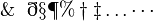
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\smile \frown \wr \triangleleft \triangleright \infty \bot \top
|
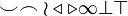
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\vdash \vDash \Vdash \models \lVert \rVert \imath \hbar
|
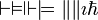
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\ell \mho \Finv \Re \Im \wp \complement
|
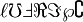
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
\diamondsuit \heartsuit \clubsuit \spadesuit \Game \flat \natural \sharp
|
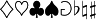
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Larger ExpressionsSubscripts, superscripts, integrals
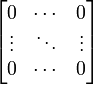
Fractions, matrices, multilines
Parenthesizing big expressions, brackets, bars
You can use various delimiters with \left and \right:
Alphabets and typefacesTexvc cannot render arbitrary Unicode characters. Those it can handle can be entered by the expressions below. For others, such as Cyrillic, they can be entered as Unicode or HTML entities in running text, but cannot be used in displayed formulas.
ColorEquations can use color:
See here for all named colors supported by LaTeX. Note that color should not be used as the only way to identify something, because it will become meaningless on black-and-white media or for color-blind people. Formatting issuesSpacingNote that TeX handles most spacing automatically, but you may sometimes want manual control.
Automatic spacing may be broken in very long expressions (because they produce an overfull hbox in TeX):
This can be remedied by putting a pair of braces { } around the whole expression:
Alignment with normal text flowDue to the default css img.tex { vertical-align: middle; }
an inline expression like If you need to align it otherwise, use Also note that if you rely on this workaround, if/when the rendering on the server gets fixed in future releases, as a result of this extra manual offset your formulae will suddenly be aligned incorrectly. So use it sparingly, if at all. Forced PNG renderingTo force the formula to render as PNG, add You can also use This could be useful to keep the rendering of formulae in a proof consistent, for example, or to fix formulae that render incorrectly in HTML (at one time, a^{2+2} rendered with an extra underscore), or to demonstrate how something is rendered when it would normally show up as HTML (as in the examples above). For instance:
You might want to include a comment in the HTML so people don't "correct" the formula by removing it:
Commutative diagramsTo make a commutative diagram, there are three steps:
Diagrams in TeXXy-pic (online manual) is the most powerful and general-purpose diagram package in TeX. Simpler packages include: The following is a template for Xy-pic, together with a hack to increase the margins in dvips, so that the diagram is not truncated by over-eager cropping (suggested in TUGboat:kpss TUGboat, Volume 17 1996, No. 3):
\documentclass{amsart}
\usepackage[all, ps, dvips]{xy} % Loading the XY-Pic package
% Using postscript driver for smoother curves
\usepackage{color} % For invisible frame
\begin{document}
\thispagestyle{empty} % No page numbers
\SelectTips{eu}{} % Euler arrowheads (tips)
\setlength{\fboxsep}{0pt} % Frame box margin
{\color{white}\framebox{{\color{black}$$ % Frame for margin
\xymatrix{ % The diagram is a 3x3 matrix
%%% Diagram goes here %%%
}
$$}}} % end math, end frame
\end{document}
Convert to SVGOnce you have produced your diagram in LaTeX (or TeX), you can convert it to an SVG file using the following sequence of commands: pdflatex file.tex pdfcrop --clip file.pdf tmp.pdf pdf2svg tmp.pdf file.svg (rm tmp.pdf at the end) If you do not have pdflatex (which is unlikely) you can also use the commands latex file.tex dvipdfm file.dvi to get a PDF version of your diagram. The pdfcrop and pdf2svg utilities are needed for this procedure. An alternative, which goes via PS rather than PDF, is: latex comm.tex dvips -E -y 2500 -o comm.eps comm.dvi eps2eps -dNOCACHE comm.eps comm2.eps pstoedit -f sk comm2.eps comm.sk inkscape -z -f comm.sk -l comm.svg These produce a DVI file, convert it to EPS (rescaling by 2.5x), convert fonts to outlines, and convert to SVG via Sketch. One advantage is that rescaling makes smaller or more complex diagrams more legible, as xy-pic normally sizes for printed matter. ProgramsIn general, you will not be able to get anywhere with diagrams without TeX and Ghostscript, and the These programs are:
Upload the fileAs the diagram is your own work, upload it.
== LaTeX source ==
<source lang="latex">
% LaTeX source here
</source>
== [[Commons:Copyright tags|Licensing]]: ==
{{self|PD-self (or other license)|author=[[User:YourUserName|Your Real Name]]}}
[[Category:Descriptive categories, such as "Group theory"]]
[[Category:Commutative diagrams]]
ExamplesA sample conforming diagram is commons:Image:PSU-PU.svg. ExamplesQuadratic Polynomial
Quadratic Polynomial (Force PNG Rendering)
Quadratic Formula
Tall Parentheses and Fractions
Integrals
Summation
Differential Equation
Complex numbers
Limits
Integral Equation
Example
Continuation and cases
Prefixed subscript
Fraction and small fraction
External links
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
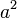
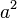
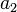
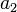
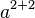
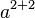
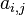
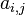
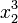
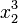
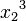
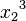
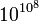
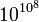
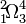
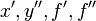
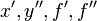
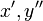
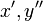
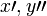
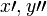
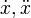
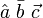
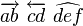
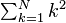
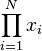
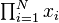
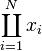
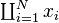
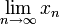
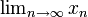
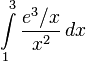
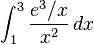
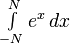
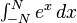
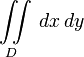
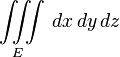
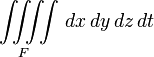
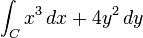
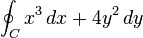
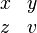
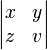
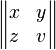
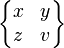
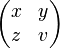
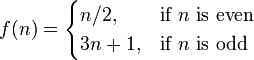
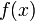
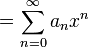
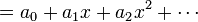
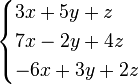

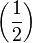

![\left [ \frac{a}{b} \right ] \quad \left \lbrack \frac{a}{b} \right \rbrack](/wiki/images/math/7/c/b/7cb5a74153ec87cdda6b92669ba685e1.png)

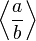
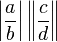
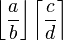
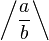
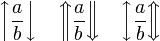
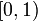
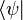
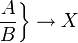
![\big( \Big( \bigg( \Bigg( \dots \Bigg] \bigg] \Big] \big]](/wiki/images/math/6/4/2/642a7988a93248dd92f1a53804cd40aa.png)

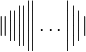

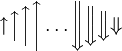
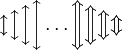

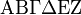
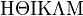
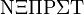
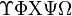
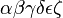
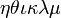
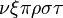
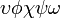
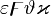
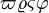
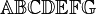
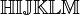
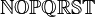
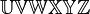
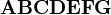
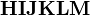
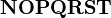
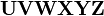
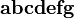
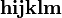
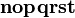
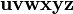
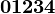
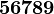
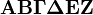
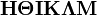
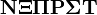
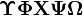
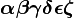
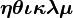
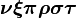
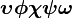
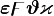
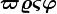
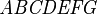
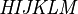
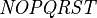
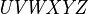
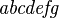
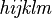
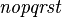
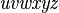
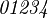
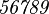
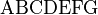
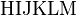
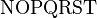
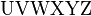
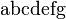
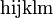
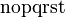
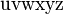
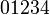
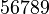
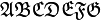
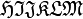
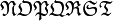
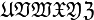
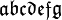
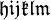
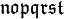
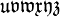
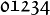
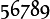
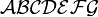
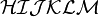
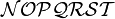
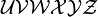
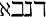
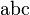
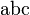
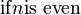
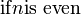
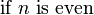
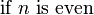
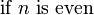
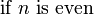
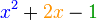
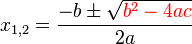


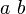
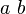
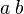
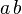
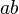
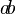
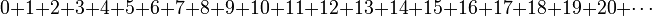
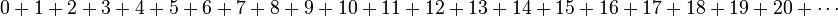
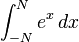 should look good.
should look good.
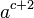
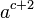
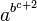 (WRONG with option "HTML if possible or else PNG"!)
(WRONG with option "HTML if possible or else PNG"!)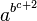 (WRONG with option "HTML if possible or else PNG"!)
(WRONG with option "HTML if possible or else PNG"!)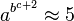 (due to "
(due to "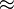 " correctly displayed, no code "\,\!" needed)
" correctly displayed, no code "\,\!" needed)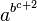
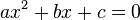 <math>ax^2 + bx + c = 0</math>
<math>ax^2 + bx + c = 0</math>
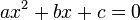 <math>ax^2 + bx + c = 0\,\!</math>
<math>ax^2 + bx + c = 0\,\!</math>
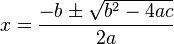 <math>x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}</math>
<math>x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}</math>
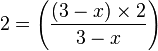 <math>2 = \left(
\frac{\left(3-x\right) \times 2}{3-x}
\right)</math>
<math>2 = \left(
\frac{\left(3-x\right) \times 2}{3-x}
\right)</math>
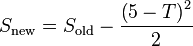 <math>S_{\text{new}} = S_{\text{old}} - \frac{ \left( 5-T \right) ^2} {2}</math>
<math>S_{\text{new}} = S_{\text{old}} - \frac{ \left( 5-T \right) ^2} {2}</math>
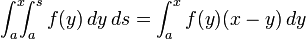 <math>\int_a^x \!\!\!\int_a^s f(y)\,dy\,ds
= \int_a^x f(y)(x-y)\,dy</math>
<math>\int_a^x \!\!\!\int_a^s f(y)\,dy\,ds
= \int_a^x f(y)(x-y)\,dy</math>
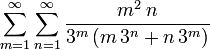 <math>\sum_{m=1}^\infty\sum_{n=1}^\infty\frac{m^2\,n}
{3^m\left(m\,3^n+n\,3^m\right)}</math>
<math>\sum_{m=1}^\infty\sum_{n=1}^\infty\frac{m^2\,n}
{3^m\left(m\,3^n+n\,3^m\right)}</math>
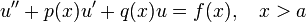 <math>u'' + p(x)u' + q(x)u=f(x),\quad x>a</math>
<math>u'' + p(x)u' + q(x)u=f(x),\quad x>a</math>
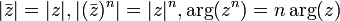 <math>|\bar{z}| = |z|,
|(\bar{z})^n| = |z|^n,
\arg(z^n) = n \arg(z)</math>
<math>|\bar{z}| = |z|,
|(\bar{z})^n| = |z|^n,
\arg(z^n) = n \arg(z)</math>
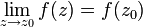 <math>\lim_{z\rightarrow z_0} f(z)=f(z_0)</math>
<math>\lim_{z\rightarrow z_0} f(z)=f(z_0)</math>
![\phi_n(\kappa)
= \frac{1}{4\pi^2\kappa^2} \int_0^\infty \frac{\sin(\kappa R)}{\kappa R} \frac{\partial}{\partial R} \left[R^2\frac{\partial D_n(R)}{\partial R}\right]\,dR](/wiki/images/math/7/f/b/7fb11db1e8b5890998b2f0f59f0e3d60.png) <math>\phi_n(\kappa) =
\frac{1}{4\pi^2\kappa^2} \int_0^\infty
\frac{\sin(\kappa R)}{\kappa R}
\frac{\partial}{\partial R}
\left[R^2\frac{\partial D_n(R)}{\partial R}\right]\,dR</math>
<math>\phi_n(\kappa) =
\frac{1}{4\pi^2\kappa^2} \int_0^\infty
\frac{\sin(\kappa R)}{\kappa R}
\frac{\partial}{\partial R}
\left[R^2\frac{\partial D_n(R)}{\partial R}\right]\,dR</math>
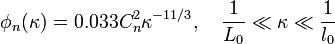 <math>\phi_n(\kappa) =
0.033C_n^2\kappa^{-11/3},\quad
\frac{1}{L_0}\ll\kappa\ll\frac{1}{l_0}</math>
<math>\phi_n(\kappa) =
0.033C_n^2\kappa^{-11/3},\quad
\frac{1}{L_0}\ll\kappa\ll\frac{1}{l_0}</math>
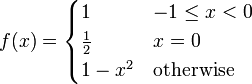 <math>
f(x) =
\begin{cases}
1 & -1 \le x < 0 \\
\frac{1}{2} & x = 0 \\
1 - x^2 & \mbox{otherwise}
\end{cases}
</math>
<math>
f(x) =
\begin{cases}
1 & -1 \le x < 0 \\
\frac{1}{2} & x = 0 \\
1 - x^2 & \mbox{otherwise}
\end{cases}
</math>
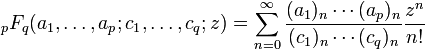 <math>{}_pF_q(a_1,\dots,a_p;c_1,\dots,c_q;z)
= \sum_{n=0}^\infty
\frac{(a_1)_n\cdots(a_p)_n}{(c_1)_n\cdots(c_q)_n}
\frac{z^n}{n!}</math>
<math>{}_pF_q(a_1,\dots,a_p;c_1,\dots,c_q;z)
= \sum_{n=0}^\infty
\frac{(a_1)_n\cdots(a_p)_n}{(c_1)_n\cdots(c_q)_n}
\frac{z^n}{n!}</math>
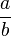
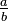 <math> \frac {a}{b}\ \tfrac {a}{b} </math>
<math> \frac {a}{b}\ \tfrac {a}{b} </math>